今回は前回のPythonでのカルマンフィルタの続きです。というか久々に数学を解いた気がしたので、紹介したいと思って記事にしました。
時間間隔が変化する場合のカルマンフィルタ
以前のカルマンフィルタは時間間隔が一定の場合の処理方法でした。でももしかしたら時間間隔が変化する計測データ(例えば、あまり重要でない時間帯は時間間隔を広く、重要な時間帯は時間間隔を短くしたい場合の計測データ)があるかもしれません。
この場合、この資料の最後の方に書かれている不当間隔時間モデルというのがあるみたいなのですが、正直難しくてわかりませんでした。その他の方法として、一番短い時間間隔に合わせる方法が考えられます。つまり、一番短い時間間隔でフィルタし続け、データがない部分はカルマン予測を行う方法です。
ただし、この場合時間間隔が短い場合に予測に時間がかかってしまう恐れがあります(下図)。
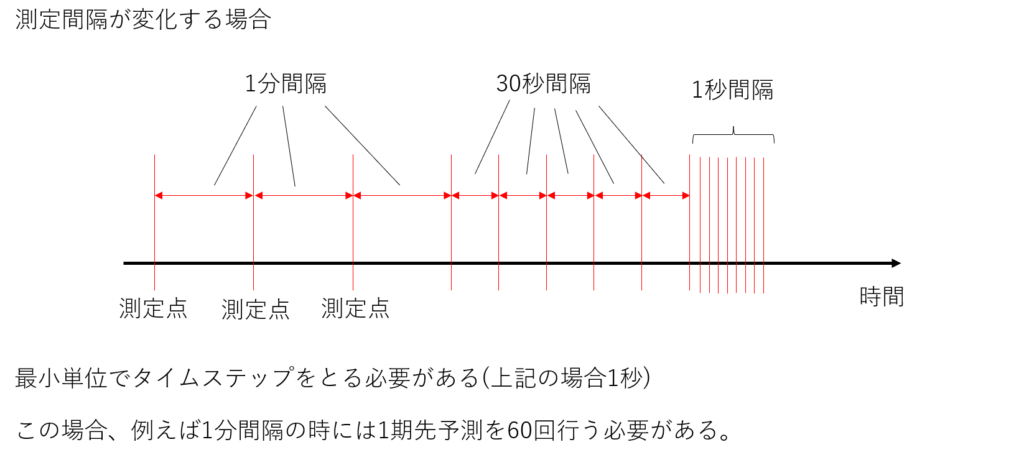
この予測のループ計算を高速化できればパラメータ算出やフィルタリングで時間がかからずに済みます(下図)。

コードでいうと以下の部分、この関数をforループで繰り替えす必要がある。
|
1 2 3 4 5 6 7 8 |
#python def kalman_prediction(a, R, W, G=G): """ Kalman prediction """ a = G @ a R = G @ R @ G.T + W return a, R |
1期先予測の高速化
1次のトレンドモデルの場合
1次のトレンドモデルの場合は簡単です。

コードで書くと、nn-1になっているのは測定点の間隔分だけ予測するようにしているからです。例えば1分間隔で測定していて、最短の1秒間隔で予測する場合、測定してから59回予測してから次の測定点になるからです。
|
1 2 3 4 5 6 7 8 |
def kalman_prediction(a, R, nn, W, G=G): """ Kalman prediction """ # a はそのまま R = R + (nn-1) * W return a, R |
2次のトレンドモデルの場合
2次のトレンドモデルの場合は難しいです。
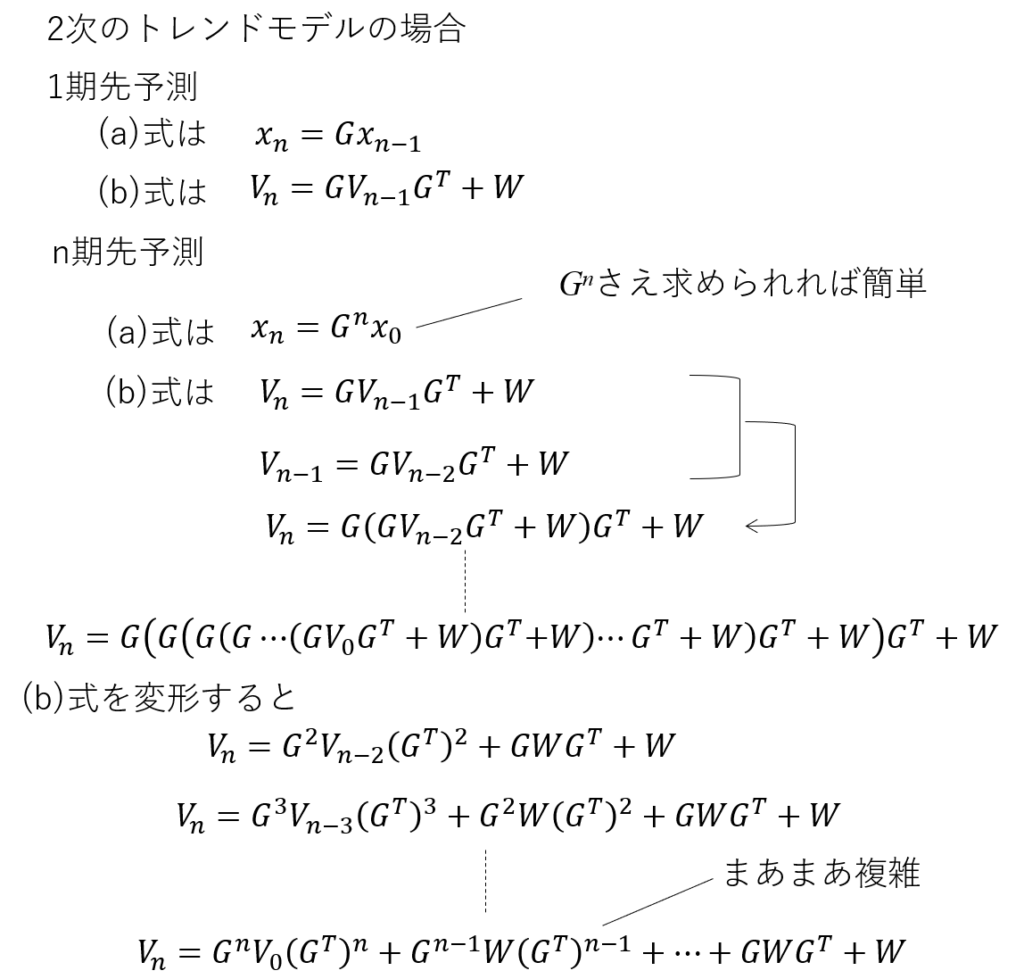
そこで以下のようにEnを仮定して漸化式を解きます。これがやりたかった!というか他に解き方があったら教えてほしいです。
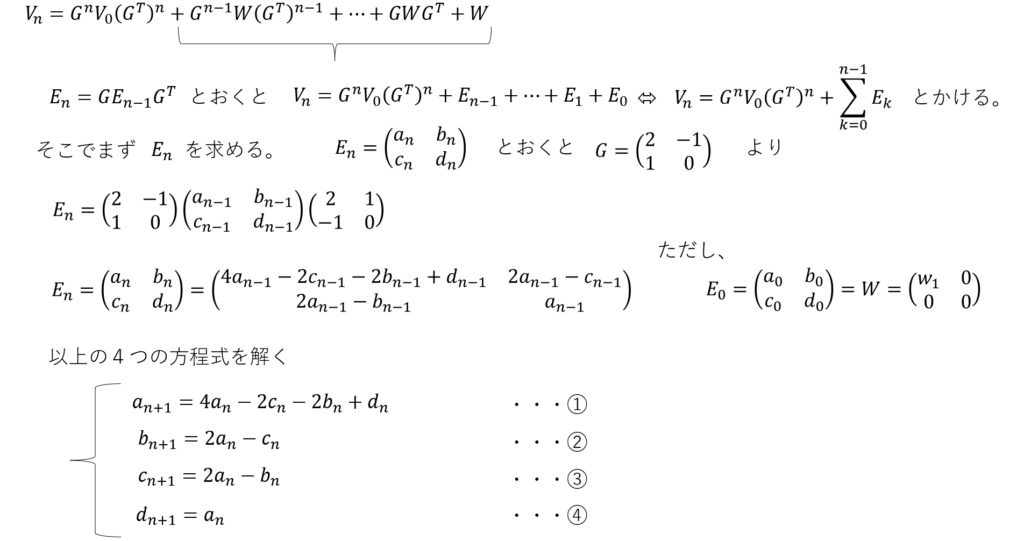
こういうの高校で数学勉強して以来だったので解いててワクワクしてしまいました。
以下僕なりの解法です。


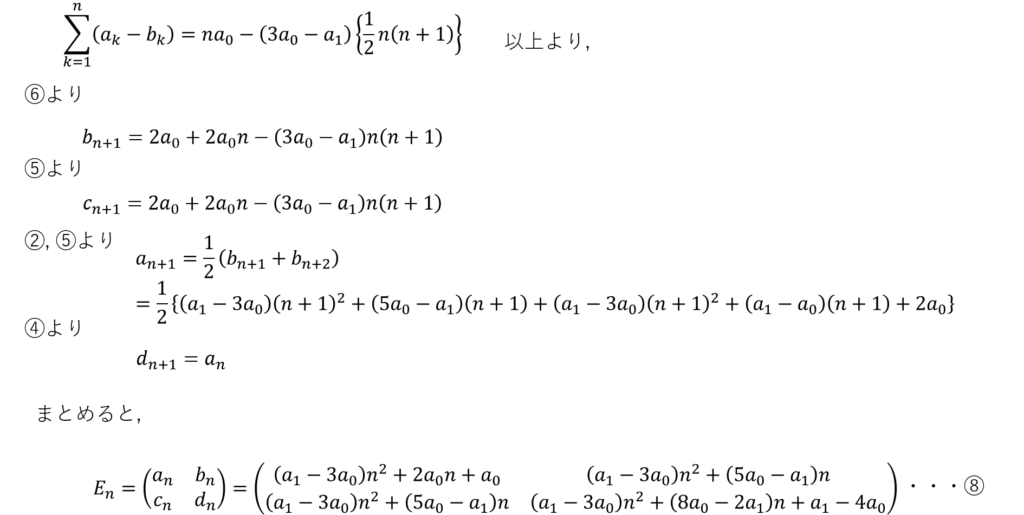
Enをnの式で表すことができました!あとは総和を求めます。


G行列のn乗についてはどうしても計算しなければいけませんが、numpyのnp.linalg.matrix_power(G,n)で高速で計算できるのでそれほど時間はかからないと思います。
コードの作成
以上の式を使ってカルマンフィルタのコードを記述します。なお、カルマン平滑化については今回考えていないので、削除しました(ごめんなさい)。
1. データの作成
今回は予め作っておいたcsvを読み込みます。中身は前回の記事で作成したものと同じですが、indexとして時間を1分間隔で作成し、400step以降は1秒間隔にしました(計1000step)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
# Python import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import scipy.optimize import datetime import matplotlib.dates as mdates import time sns.set_style('darkgrid') #G = np.array([[1,0],[0,0]]) # システムモデルの係数行列(1次のトレンドモデル) G = np.array([[2,-1],[1,0]]) # システムモデルの係数行列(2次のトレンドモデル) F = np.array([[1,0]]) # 観測モデルの係数行列 T = 1000 #最大時間 x0 = 0 #初期値 Tr = 0 #尤度算出のためのトリガー(Tr=1で尤度算出用) data = pd.read_csv('input.csv', header=0, index_col=0, encoding='shift_jis',parse_dates=True) # csv読み込み,parse_datas=Trueでdatetime型に変換 x = data.index # インデックス y_true = data.iloc[:,0].values # 真値 y_obs = data.iloc[:,1].values # 観測データ fig, ax = plt.subplots(nrows=1, figsize=(16, 6)) plt.title("Test Data") sns.lineplot(x=x, y=y_obs, color="gray", label="observation", ax=ax) sns.lineplot(x=x, y=y_true, color="black", label="true value", ax=ax) ax.axvline(datetime.datetime(2021, 11, 15, hour=4, minute=0, second=0), color="blue", linestyle="--", alpha=0.5) ax.axvline(datetime.datetime(2021, 11, 15, hour=4, minute=1, second=10), color="red", linestyle="--", alpha=0.5) ax.axvline(datetime.datetime(2021, 11, 15, hour=4, minute=2, second=1), color="red", linestyle="--", alpha=0.5) locator = mdates.HourLocator(interval=1) formatter = mdates.ConciseDateFormatter(locator) ax.xaxis.set_major_locator(locator) ax.xaxis.set_major_formatter(formatter) plt.show() fig.savefig("data.png", transparent = True, bbox_inches = 'tight', pad_inches = 0) |
出力図は以下の通り、見ずらいですが、青点線で時間間隔が変わっていて、赤間隔の間が観測データがないところです。
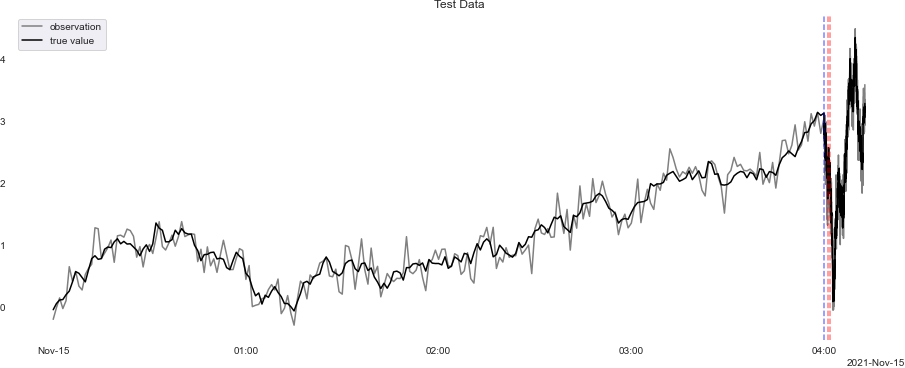
2. カルマンフィルタ(1期先予測・フィルタ)の作成
1期先予測とフィルタのコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# Python def kalman_prediction(a, R, mn, W, G=G): """ Kalman prediction """ #*******************************1次のトレンドモデルの場合 # R = R + (mn-1) * W #******************************* #*******************************2次のトレンドモデルの場合 nn = mn - 1 w_nn = W[0,0]*(nn-1)*nn*(2*nn-1)/6 E = np.array([[w_nn+W[0,0]*(nn-1)*nn+W[0,0]*(nn-1)+W[0,0],w_nn+0.5*W[0,0]*(nn-1)*nn],[w_nn+0.5*W[0,0]*(nn-1)*nn,w_nn]]) A = np.linalg.matrix_power(G,nn) A_T =np.linalg.matrix_power(G.T,nn) a = A @ a R = A @ R @ A_T + E #******************************* #*******************************これまでの方法 # for i in range(td-1): # a = G @ a # R = G @ R @ G.T + W #******************************* return a, R |
3. パラメータ推定(最尤推定法)
ほぼ変わってないですが、前時刻と今時刻を比較してその差が2秒以上あればその分予測をするようにしています。1秒以下の場合はこの行程をスキップして観測値がなければ予測、あればフィルタの処理を行っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
#Python def calcLogLike(sigma, times): # 尤度算出用 LLF = 0. # 尤度 m0 = np.array([0.0, 0.0]) # 状態変数の初期値 C0 = np.array([[1e7,0],[0,1e7]]) # 状態変数の共分散行列の初期値 m = np.zeros((T, 2)) # 状態変数 C = np.zeros((T, 2, 2)) # 状態変数の共分散行列 sigma_exp = np.exp(sigma) # システムノイズと観測ノイズの分散の値 WL = np.array([[sigma_exp[0],0],[0,0]]) # システムノイズ VL = np.array([[sigma_exp[1]]]) # 観測ノイズ for t in range(times): if t == 0: #初期 m[t], C[t], L = kalman_filter(m0, C0, y_obs[t], W=WL , V=VL, Tr=1) LLF += -0.5*(1.*np.log(2.*np.pi) + L[0]) #尤度算出 else: start_date = data.index[t-1] #扱うデータの前の時刻 end_date = data.index[t] #扱うデータの時刻 td = end_date - start_date #前のデータからの時刻の差分 m_inp = np.copy(m[t-1]) C_inp = np.copy(C[t-1]) minu = int(td.total_seconds()) #秒刻み if minu >= 2: #1秒未満は1秒として計算される m_pre, C_pre = kalman_prediction(m[t-1], C[t-1], minu, W=WL) m_inp = np.copy(m_pre) C_inp = np.copy(C_pre) if np.isnan(y_obs[t]): # 観測値がない場合は予測を実行 m[t], C[t] = kalman_prediction(m_inp, C_inp, 2, W=WL) else: m[t], C[t], L = kalman_filter(m_inp, C_inp, y_obs[t], W=WL , V=VL, Tr=1) LLF += -0.5*(1.*np.log(2.*np.pi) + L[0]) #尤度算出 return -LLF # L-BFGS-B bounds = ((-40.,1.), (-20.,1.)) #変数の範囲 times = 500 #尤度算出に時刻いつまでを使うか result = scipy.optimize.minimize(calcLogLike, x0=[-10.0, -10.0], method="L-BFGS-B", bounds = bounds, args=(times,)) W1_predict = np.exp(result.x[0]) # システムノイズの分散 V1_predict = np.exp(result.x[1]) # 観測ノイズの分散 start = time.time() result_fun = calcLogLike(sigma=[result.x[0],result.x[1]],times = times) process_time = time.time() - start print('process_time = ', process_time) print('W1_predict = {0:.6g}, V1_predict = {1:.6g}, likelihood = {2:.6g}'.format(W1_predict, V1_predict, -result_fun)) # 差分進化 # bounds = ((-40.,1.), (-20.,1.)) #変数の範囲 # time = 500 #尤度算出に時刻いつまでを使うか # result = scipy.optimize.differential_evolution(calcLogLike, bounds = bounds, args=(times,)) # W1_predict = np.exp(result.x[0]) # システムノイズの分散 # V1_predict = np.exp(result.x[1]) # 観測ノイズの分散 # result_fun = calcLogLike(sigma=[result.x[0],result.x[1]],times = times) # print('W1_predict = {0:.6g}, V1_predict = {1:.6g}, likelihood = {2:.6g}'.format(W1_predict, V1_predict, -result_fun)) |
4. カルマンフィルタの実行
インデックスを比較して秒刻みで予測とフィルタを行うようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#Python # カルマンフィルター+カルマン予測 内容尤度算出と同じ for t in range(T): if t == 0: m[t], C[t] = kalman_filter(m0, C0, y_obs[t], W=WL , V=VL) else: start_date = data.index[t-1] #扱うデータの前の時刻 end_date = data.index[t] #扱うデータの時刻 td = end_date - start_date #前のデータからの時刻の差分 m_inp = np.copy(m[t-1]) C_inp = np.copy(C[t-1]) minu = int(td.total_seconds()) #秒刻み if minu >= 2: #1秒未満は1秒として計算される m_pre, C_pre = kalman_prediction(m[t-1], C[t-1], minu, W=WL) m_inp = np.copy(m_pre) C_inp = np.copy(C_pre) if np.isnan(y_obs[t]): m[t], C[t] = kalman_prediction(m_inp, C_inp, 2, W=WL) else: m[t], C[t] = kalman_filter(m_inp, C_inp, y_obs[t], W=WL , V=VL) |
5. 図化+出力
図化と出力です。平滑化を省きました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#Python upper = 5 lower = -1 x_min = 0 x_max = 1000 legend_loc = "upper left" fig, axes = plt.subplots(nrows=1, figsize=(16, 8)) sns.lineplot(x=x, y=y_obs, color="gray", ax=axes, label="observation") sns.lineplot(x=x, y=m[:,0].flatten(), color="red", ax=axes, label="kalman filter + prediction") sns.lineplot(x=x, y=y_true.flatten(), color="black", ax=axes, label="true value") axes.plot(x, (m[:,0] - 1.96 * C[:,0,0]**(1/2)).flatten(), alpha=0.3, color='gray', label=".95 interval") axes.plot(x, (m[:,0] + 1.96 * C[:,0,0]**(1/2)).flatten(), alpha=0.3, color='gray') locator = mdates.HourLocator(interval=1) formatter = mdates.ConciseDateFormatter(locator) axes.xaxis.set_major_locator(locator) axes.xaxis.set_major_formatter(formatter) #axes[0].axvline(310, color="black", linestyle="--", alpha=0.5) #axes[0].axvline(360, color="black", linestyle="--", alpha=0.5) axes.set_ylim(lower, upper) #axes.set_xlim(x_min, x_max) axes.legend(loc=legend_loc) axes.set_title("Kalman Filter + Prediction") plt.show() fig.savefig("result.png", transparent = True, bbox_inches = 'tight', pad_inches = 0) # 出力関係 df = pd.DataFrame(np.concatenate([x.reshape(T,1), y.reshape(T,1), m[:,0].reshape(T,1)], 1)) df.columns=["true value", "obsevation", "kalman filter"] df.to_csv("output.csv") |
図化したグラフがこれ
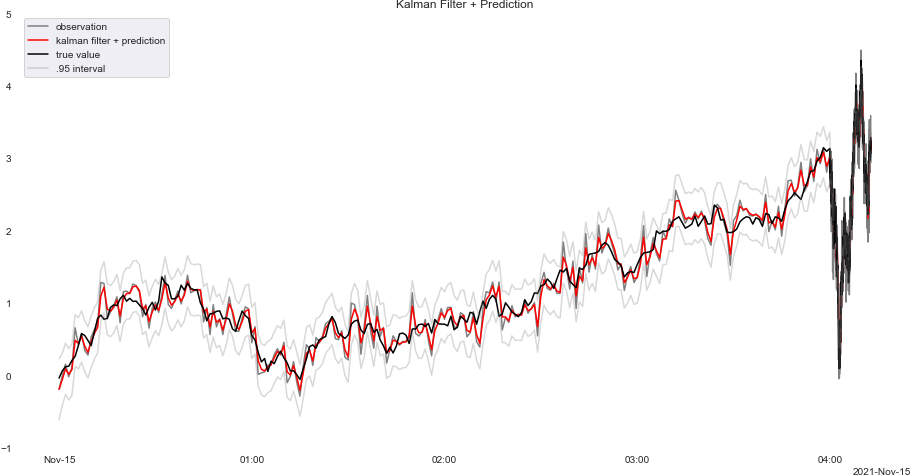
ん~微妙かも、予測が多すぎるのも良くないんですかね?まあ計算できるってことでよし
時間の比較
通常の方法と比較して計算してみた結果、尤度推定にかかる時間は通常の場合で0.1426秒、上述の方法では0.0688秒でした。半分くらいの時間ですね。多分もっと長い時間であれば効果がより確認できると思います。
今回の短いステップ数でもこれだけ差がでるので十分だと思います。
まとめ
今回はカルマンフィルタの1期先予測で高速に計算する方法を考えてみました。
今後もカルマンフィルタについて勉強していきたいと思いますので、よろしくお願いします。
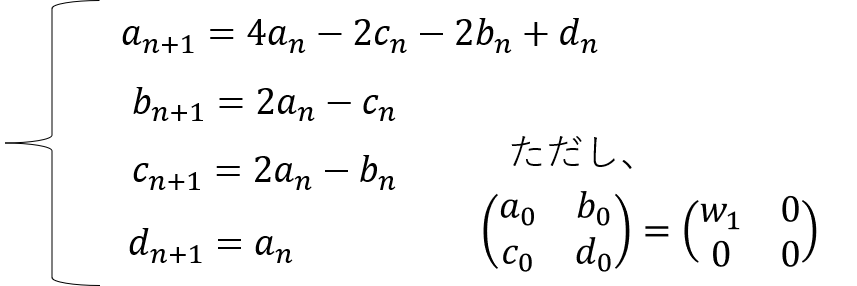



コメント