前回からまた大分時間が経ってしまいましたが、今回は非ガウス型カルマンフィルタの実装ということで、やってみたいと思います。
非線形・非ガウス型カルマンフィルタ
非線形・非ガウス型カルマンフィルタについては、こちらの動画やこちらのサイトやこちらの資料を見られると良いかもしれません。まあ難しい。私はこちらの本を買って読んで見たのですが、なかなか難しく、ちゃんと勉強する方には良いかもしれませんが、私のような新参ものが理解するには少々難儀します。
といっても実装したい意志はかわらないので、いろいろな資料を紐解きつつ実装してみました。
非線形・非ガウス型カルマンフィルタはこれまでの線形カルマンフィルタの手順では解けないもので、ノイズの分布が正規分布でなかったり、システム方程式が非線形であったりする場合に使用するものです。
私がやりたかったのは、システムノイズがコーシー分布である状態方程式で、これは通常の線形カルマンフィルタでは解けません。
非線形・非ガウス型カルマンフィルタを解く方法は色々あるみたいで、一番一般的なものは拡張カルマンフィルタという非線形の部分を線形に近似して解く方法です。ただこちらの方法で私のやりたかったことを実現することはできませんでした(私の実力不足の可能性もあります)。
その他にもアンサンブルカルマンフィルタやパーティクルフィルタなどがありました。ただこの2つは私の知る限りでは乱数を発生させるため再現性がありません。また、私がやりたかったことは、何度やっても同じ結果を再現したいということでしたので、別の方法を模索しました。
そして今回行き着いたのが、階段関数によるカルマンフィルタです。詳しい解説はこちらの資料の46p以降に書いてあります。分布を細かく区分して、システムノイズ分布や観測ノイズ分布と畳み込み積分を使って事象の確率分布を計算するものです。
計算手順
簡単のため1次のトレンドモデルの場合について、手順を記載します。上記のサイトとほぼ同じなので、必要ない方は飛ばしてください。

フィルタと1期先予測は以下のとおりです。


規格化については、 各ステップの後で密度関数の全積分 が1になるように行います。
以上を繰り返します、平滑化については、今回も割愛します。
コードの作成
以上の計算をPythonで実装していきます。
1. データの作成
今回は予め作っておいたcsvを読み込みます。
今回は途中(11/3 03:00)でデータが急上昇するモデルにしました。こういったモデルの場合は正規分布では対応しきれないことがあるため、コーシー分布を使うほうが良い場合もあります。
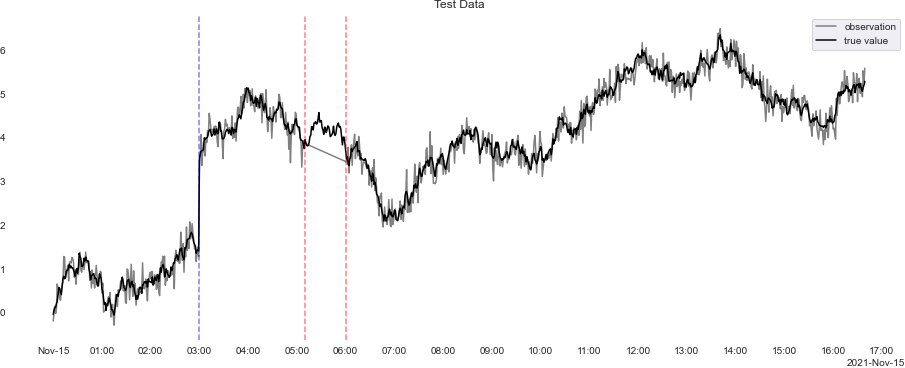
コードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# Python import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import scipy.optimize from scipy import stats from scipy import interpolate from tqdm import tqdm_notebook as tqdm from matplotlib import cm import time import datetime import matplotlib.dates as mdates pd.set_option('display.max_columns', None) sns.set_style('darkgrid') G = np.array([[1,0],[0,0]]) # システムモデルの係数行列(1次のトレンドモデル) #G = np.array([[2,-1],[1,0]]) # システムモデルの係数行列(2次のトレンドモデル) F = np.array([[1,0]]) # 観測モデルの係数行列 T = 1000 #最大時間 x0 = 0 #初期値 Tr = 0 #尤度算出のためのトリガー(Tr=1で尤度算出用) data = pd.read_csv('input_stear.csv', header=0, index_col=0, encoding='shift_jis',parse_dates=True) # csv読み込み,parse_datas=Trueでdatetime型に変換 x = data.index # インデックス y_true = data.iloc[:,0].values # 真値 y_obs = data.iloc[:,1].values # 観測データ fig, ax = plt.subplots(nrows=1, figsize=(16, 6)) plt.title("Test Data") sns.lineplot(x=x, y=y_obs, color="gray", label="observation", ax=ax) sns.lineplot(x=x, y=y_true, color="black", label="true value", ax=ax) ax.axvline(datetime.datetime(2021, 11, 15, hour=3, minute=0, second=0), color="blue", linestyle="--", alpha=0.5) ax.axvline(datetime.datetime(2021, 11, 15, hour=5, minute=10, second=0), color="red", linestyle="--", alpha=0.5) ax.axvline(datetime.datetime(2021, 11, 15, hour=6, minute=0, second=0), color="red", linestyle="--", alpha=0.5) locator = mdates.HourLocator(interval=1) formatter = mdates.ConciseDateFormatter(locator) ax.xaxis.set_major_locator(locator) ax.xaxis.set_major_formatter(formatter) plt.show() fig.savefig("data.png", transparent = True, bbox_inches = 'tight', pad_inches = 0) # 8÷0.02=400要素で分割する space_d = 8 #幅4m d_t = 0.02 #ステップ幅0.02m |
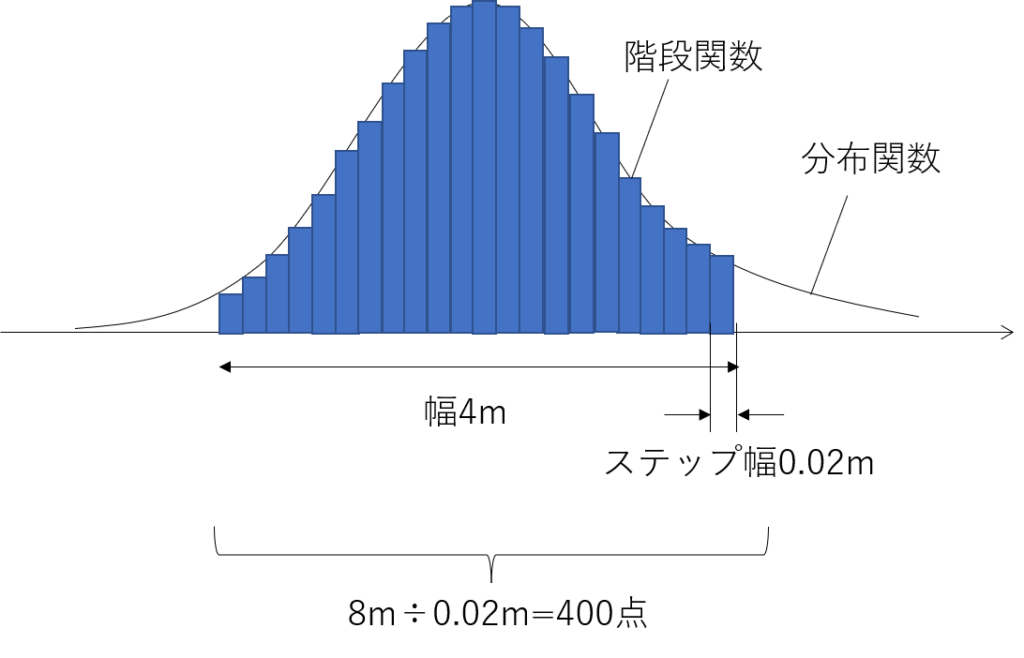
これまでと違う部分は一番下の部分です。意味的には以下の図の通りで、階段関数で近似する幅と一つ一つのステップ幅を定義しています。
2. カルマンフィルタ(1期先予測・フィルタ)の作成
1期先予測とフィルタのコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
#Python def kalman_prediction(q,f,nn,Q): """ Kalman prediction """ #***************************************************#通常通り畳み込み積分をする場合 # for k in range(nn-1): # pp = np.zeros(len(f)) # 予測分布の格納配列 # for i in range(len(f)): # for j in range(len(f)): # pp[i] += d_t*q[len(f)+i-j]*f[j] # pp = pp/np.sum(pp)/d_t # f = pp #***************************************************#行列を使って畳み込み積分をする場合 Q_N = np.linalg.matrix_power(d_t*Q,nn-1) pp = np.zeros(len(f)) # 予測分布の格納配列 pp = Q_N @ f pp = pp/np.sum(pp)/d_t #*************************************************** return pp def kalman_filter(f,step,y,q,v,Q, Tr=Tr): """ Kalman Filter """ C = 0. # 規格化定数 ff = np.zeros(len(f)) # フィルタ分布の格納配列 pp = np.zeros(len(f)) # 予測分布の格納配列 r = np.exp(-(y-step)**2/(2*v))/np.sqrt(2.*np.pi*v) # 観測ノイズ #予測 pp = d_t*Q @ f pp = pp/np.sum(pp)/d_t #フィルタリング ff = r * pp C = sum(ff)*d_t if Tr == 1: if C <= 0: # 規格化定数が0以下の場合は適切でない return pp,ff, 999999 else: ff = ff/C ff = ff/np.sum(ff)/d_t return pp,ff, C else: ff = ff/C ff = ff/np.sum(ff)/d_t return pp,ff |
予測の関数内でそのまま計算する方法を記載していますが、計算を高速化するために、以下の通り予めシステムノイズの行列Qを作成しておいて、それを利用して計算しています。以下を計算することでn期先予測も1回の積で計算できます。Qの計算自体は次の過程で行っています。

その他予測の計算を高速化する方法として、畳み込み積分に高速フーリエ変換を使って計算する方法等もありますが、上記の方法のほうが早かったため今回は記載していません。詳しくはこちらのサイトを御覧ください。
3. パラメータ推定(最尤推定法)
最尤推定法自体はこれまでの方法と同じです。step配列はフィルタ分布等のx座標を格納する配列です。この方法では階段関数の幅(今回は8m)が1回の計算のたびに移動することを想定しているため、stepの値が移動していきます。calcLogLike関数の最後がその部分です。フィルタの平均値を中央としてその前後(今回は前後4m)をstep幅として移動させています。移動させるにあたって端の部分に関しては線形近似を行い値が負になるところは0にしています。このあたりの値のとり方によっては値が大きく変化するような変化がある場合には影響を受けてしまうところだと思います。色々試したのですが、この方法が安定していましたので、これにしました。本来は計算メモリが足りるのであれば、予想される範囲すべてをもとからモデル化しstepが移動しないようにするのが正確であるように思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
#Python def calcLogLike(sigma, times): LLF = 0. #尤度 cent_y = np.round(y_obs[0], decimals=1) ww = np.exp(sigma[0]) vv = np.exp(sigma[1]) step0 = np.arange(cent_y-space_d//2, cent_y+space_d//2, d_t) #初期状態のステップ(データの値を中央にしている) step = np.zeros((T,len(step0))) #ステップの時系列を格納する配列 step[0] = np.arange(cent_y-space_d//2, cent_y+space_d//2, d_t) #時間0はstep0と同じ p0 = np.exp(-(step0-y_obs[0])**2/(2*1e1))/np.sqrt(2.*np.pi*1e1) # 初期状態の予測分布 p = np.zeros((T,len(step[0]))) # 予測分布の時系列を格納する配列 f0 = np.exp(-(step0-y_obs[0])**2/(2*1e1))/np.sqrt(2.*np.pi*1e1) # 初期状態のフィルタリング分布 f = np.zeros((T,len(step0))) # フィルタリング分布の時系列を格納する配列 q = np.linspace(-space_d, space_d, 2*len(step0)+1) # システムノイズ分布を格納する配列 q = np.exp(-(q)**2/(2*ww))/np.sqrt(2.*np.pi*ww) # システムノイズ分布が正規分布の場合 #q = ww/(np.pi*(q**2+ww**2)) # システムノイズ分布がコーシー分布の場合 Q = np.zeros((len(f0),len(f0))) # システムノイズ分布を計算するときの行列 for i in range(len(f0)): Q[i,:] = q[i+1:i+1+len(f0)][::-1] for t in range(int(times)): #最適化のための期間 f_inp=np.zeros(len(f0)) if t == 0: p[t],f[t], L = kalman_filter(f0,step[0], y_obs[t],q,vv,Q, Tr=1) LLF += np.log(L) #尤度関数の計算 else: if np.isnan(y_obs[t]): #データがない場合予測のみ行う p[t] = kalman_prediction(q, f[t-1],2,Q) f[t,:] = p[t,:] else: #データがある場合フィルタ処理を行い尤度を計算 p[t],f[t], L = kalman_filter(f[t-1], step[t-1], y_obs[t],q,vv,Q, Tr=1) LLF += np.log(L) #尤度関数の計算 #******線形補間法 cent_y = np.round(d_t*np.dot(f[t],step[t-1]), decimals=2) step_d = np.arange(len(step0))*d_t#np.arange(cent_y-space_d, cent_y+space_d,d_t) step_d = step_d-step_d[len(step0)//2]+cent_y pho = interpolate.interp1d(step[t-1], f[t], kind='linear', fill_value='extrapolate') f[t] = pho(step_d) f[t] = np.where(f[t]<0,0,f[t]) #0以下は0にする step[t] = step_d #****** return -LLF # #L-BFGS-B t0 = time.time() bounds = ((-5.,-3), (-10.,1)) times = 500 result = scipy.optimize.minimize(calcLogLike, bounds=bounds, x0=[-4.0, 0.0], args=(times,), method="L-BFGS-B") #print(result) W_predict = np.exp(result.x[0]) V_predict = np.exp(result.x[1]) print('W_predict = %f V_predict = %f' % (W_predict, V_predict)) t1 = time.time() # 計測終了時間 elapsed_time = t1 - t0 # 経過時間 print(elapsed_time) # 経過時間を表示 |
4.カルマンフィルタの実行
未知数が決まったらあとはカルマンフィルタを実行するだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
#Python # 初期状態の作成(尤度計算と同じ) cent_y = np.round(y_obs[0], decimals=1) ww = W_predict vv = V_predict step0 = np.arange(cent_y-space_d//2, cent_y+space_d//2, d_t) step = np.zeros((T,len(step0))) step[0] = np.arange(cent_y-space_d//2, cent_y+space_d//2, d_t) p0 = np.exp(-(step0-y_obs[0])**2/(2*1e1))/np.sqrt(2.*np.pi*1e1) p = np.zeros((T,len(step[0]))) f0 = np.exp(-(step0-y_obs[0])**2/(2*1e1))/np.sqrt(2.*np.pi*1e1) f = np.zeros((T,len(step0))) q = np.linspace(-space_d, space_d, 2*len(step0)+1) q = np.exp(-(q)**2/(2*ww))/np.sqrt(2.*np.pi*ww) #q = ww/(np.pi*(q**2+ww**2)) Q = np.zeros((len(f0),len(f0))) for i in range(len(f0)): Q[i,:] = q[i+1:i+1+len(f0)][::-1] # カルマンフィルター for t in range(int(T)): #最適化のための期間 f_inp=np.zeros(len(f0)) if t == 0: p[t],f[t] = kalman_filter(f0,step[0], y_obs[t],q,vv,Q) else: if np.isnan(y_obs[t]): #データがない場合予測のみ行う p[t] = kalman_prediction(q, f[t-1],2,Q) f[t,:] = p[t,:] else: #データがある場合フィルタ処理を行い尤度を計算 p[t],f[t] = kalman_filter(f[t-1], step[t-1], y_obs[t],q,vv,Q) #******線形補間法 cent_y = np.round(d_t*np.dot(f[t],step[t-1]), decimals=2) step_d = np.arange(len(step0))*d_t#np.arange(cent_y-space_d, cent_y+space_d,d_t) step_d = step_d-step_d[len(step0)//2]+cent_y pho = interpolate.interp1d(step[t-1], f[t], kind='linear', fill_value='extrapolate') f[t] = pho(step_d) f[t] = np.where(f[t]<0,0,f[t]) step[t] = step_d #****** m = d_t*np.sum(f * step,1) # フィルタ分布の平均値を取る |
特段変わったことはないです。
5. 図化+出力
図化と出力です。平滑化を省きました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
#Python upper = -2 lower = -15 x_min = datetime.datetime(2021, 11, 15, hour=2, minute=0, second=0) x_max = datetime.datetime(2021, 11, 15, hour=4, minute=0, second=0) legend_loc = "lower left" fig, axes = plt.subplots(nrows=2, figsize=(16, 12)) #sns.lineplot(x=np.arange(T+K), y=x, ax=axes[0], label="true state") sns.lineplot(x=x, y=y_obs, color="gray", ax=axes[0], label="observation") sns.lineplot(x=x, y=y_true, color="black", ax=axes[0], label="true value") sns.lineplot(x=x, y=m[:].flatten(), color="red", ax=axes[0], label="kalman filter + prediction") #axes.set_ylim(lower, upper) #axes.set_xlim(x_min, x_max) axes[0].legend(loc=legend_loc) axes[0].set_title("Kalman Filter + Prediction") sns.lineplot(x=x, y=y_obs, color="gray", ax=axes[1], label="observation") sns.lineplot(x=x, y=y_true, color="black", ax=axes[1], label="true value") sns.lineplot(x=x, y=m[:].flatten(), color="red", ax=axes[1], label="kalman filter + prediction") axes[1].set_xlim(x_min, x_max) axes[1].legend(loc=legend_loc) axes[1].set_title("Kalman Filter + Prediction") plt.show() fig.savefig("result.png", transparent = True, bbox_inches = 'tight', pad_inches = 0) df = pd.DataFrame(np.concatenate([y_true.reshape(T,1), y_obs.reshape(T,1), m[:].reshape(T,1)], 1)) df.columns=["true value", "obsevation", "kalman filter"] df.to_csv("output.csv") |
図化したグラフが以下です。下は急激に上昇している部分を拡大したものです。
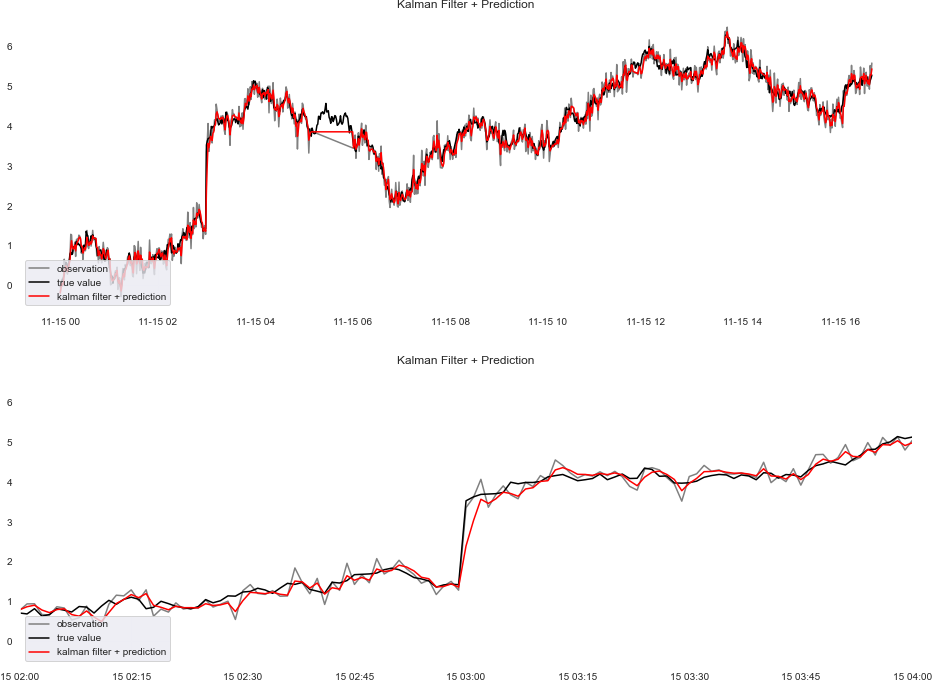
正規分布とコーシー分布の比較
これまでの計算はシステムノイズの分布を正規分布としていましたが、コーシー分布として計算し、図化したものが以下の通り、コードで変更したのは尤度計算のqをシステムノイズ分布がコーシー分布の場合に変更したのとカルマンフィルタ実行の同様qの部分をシステムノイズ分布がコーシー分布の場合に変更しただけです。
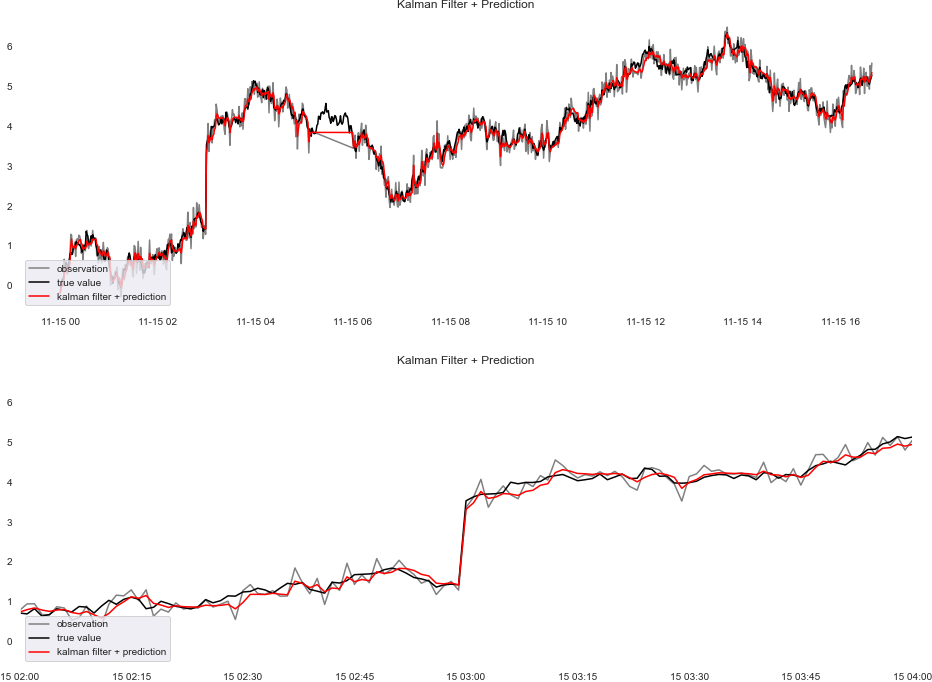
先程の正規分布と比較すると、急激に上昇する部分でより真値に近い値にすり寄っている様子がわかると思います。これがコーシー分布にした利点です。
timestep500までの尤度は正規分布=-83.12623、コーシー分布=-58.94126でコーシー分布の方が尤度が大きい結果となりました。
今回算出したシステムノイズの正規分布(赤色)とコーシー分布(緑色)を比較したものが以下の図です。下はy軸を拡大したものです。
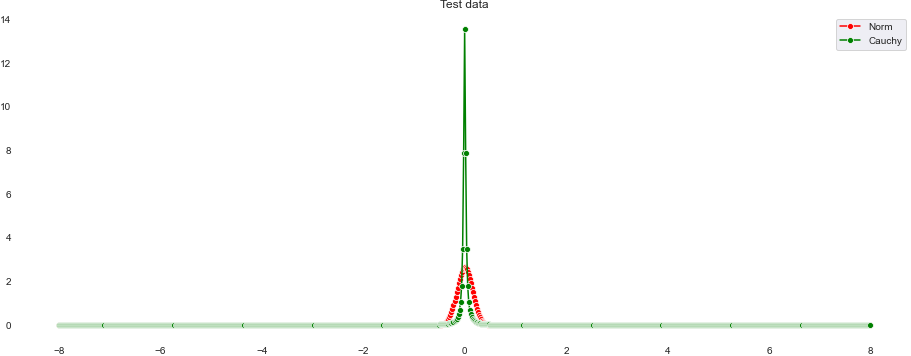
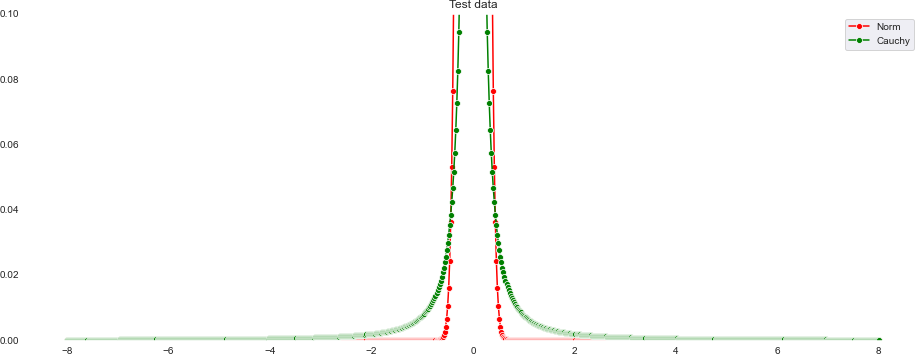
コーシー分布は正規分布に比べて裾野が広がっている様子がわかると思います。これのおかげて急激な上昇にも対応できるといったわけです。
まとめ
今回は非ガウス型カルマンフィルタということで、階段関数を用いたPythonでの実装をしてみました。メリットとしてはシステムノイズの分布がコーシー分布の場合でも計算できるところですね。デメリットとしては、ある程度幅を大きく取らないと急激な変化に対応できないため、先の観測値が予測できない場合には使用するのが難しいところと分布の細分化について、コーシー分布の中心ではかなり尖った分布形状になります。そのためステップ幅を小さく取らないと計算に誤差が出てしまう恐れがあると思います。ただし細かくしすぎるとメモリが大きくなって計算にも時間がかかってしまうと思います。このあたりはとても難しい問題だと思います。また、今回のように幅が観測値によって移動する場合には端の取り扱いも難しい問題になると思います。
完全に独学で実装したので、間違っているところがあると思いますが、意見をいただければ幸いです。今後はまた非線形カルマンフィルタの別の方法についても検討したいと思っておりますので、形になったら記事にしたいと思います。


コメント
カルマンフィルタのPythonコーディングに関する記事を拝読させていただき,感銘を受けています.
初学者のため,とりあえずコードをjupyter notebookにコピペして実行してみている程度なのですが,最後の
5. 図化+出力
のパートで下記のエラーとなってしまいます:
NameError Traceback (most recent call last)
in
11 sns.lineplot(x=x, y=y_obs, color=”gray”, ax=axes[0], label=”observation”)
12 sns.lineplot(x=x, y=y_true, color=”black”, ax=axes[0], label=”true value”)
—> 13 sns.lineplot(x=x, y=m[:].flatten(), color=”red”, ax=axes[0], label=”kalman filter + prediction”)
14 #axes.set_ylim(lower, upper)
15 #axes.set_xlim(x_min, x_max)
NameError: name ‘m’ is not defined
確かにそれ以前のパートで変数mは定義されていないようですので,正しい変数名をお教えいただければ幸いです.
たつやさん
はじめましてあしかぺんぎんと申します。
ご返信がおそくなって申し訳ございません。
まさかこんな記事を見てくれている方がいるとは思っておりませんでした。ありがとうございます。
ご指摘誠にありがとうございます。
ご指摘の通りmを計算するコードが抜けておりました。
“4.カルマンフィルタ実行”の最後にm = d_t*np.sum(f * step,1)を追加しました。
フィルタ分布の平均値をとっているだけです。
ご確認いただければ幸いです。
よろしくお願いいたします。