やりたいことが色々あるんですが、全部中途半端になってます。てことで、今日は時系列データのノイズ除去を目的として、カルマンフィルタの実装をしてみたいと思います。今後オーソドックスな線形カルマンフィルタに加えて非線形カルマンフィルタについても実装方法を記事にできたらなと思ってます。
カルマンフィルタとは
カルマンフィルタは、ルドマン・カルマンによって提唱されたアルゴリズムで、時系列を表現するモデルである、状態空間モデルを逐次的に計算するものみたいです。詳しくは調べればいくらでも出てくるのでここでは、実際の実装をメインに進めていきたいと思います。
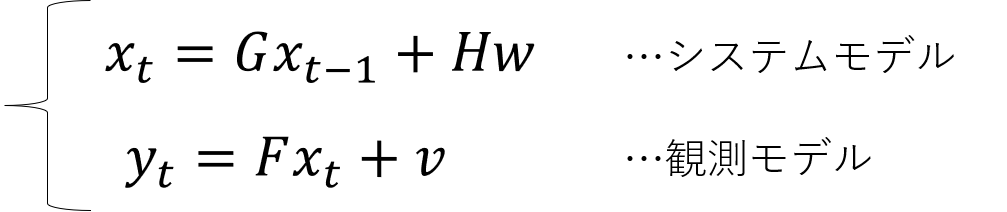
xは真値、yは観測値、wとvはノイズ、残りのG,H,Fは係数の行列で変数の書き方は教科書によって違いますが、つまりは、観測値yが得られた状態で、ノイズに紛れた本当に知りたい値である真値xを効率よく推定するアルゴリズムです。
今回はシステムモデルに1次 or 2次のトレンドモデルを切り替えて使えるようにしました。

一応1期先予測とフィルタ、平滑化の計算方法を以下に書いておきます。真値の共分散行列がVとなっておりますが、コード内ではCになっています。

実装の流れ
実装の流れを簡単に示します。ベースはこちらのサイトです。ていうかほぼここを参考にしました。それに加えてパラメータの推定や欠損値がある場合の処理を行いより実践に近いものを作ればと思います。
- データの作成
- カルマンフィルタ(1期先予測・フィルタ・平滑化)の作成
- パラメータ推定(最尤推定法)
- カルマフィルタの実行
- 図化+出力
プログラム作成
1. データの作成
まずは今回使うデータを作成します。実際に使用する場合はcsvとかから読み込むことになると思います。jupyter notebookで書いたままになります。適宜書き換えて使ってください。1次、2次のトレンドモデルの使い分けは9行目と10行目の一方をコメントアウトだけで大丈夫です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
#python import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import scipy.optimize sns.set_style('darkgrid') G = np.array([[1,0],[0,0]]) # システムモデルの係数行列(1次のトレンドモデル) #G = np.array([[2,-1],[1,0]]) # システムモデルの係数行列(2次のトレンドモデル) F = np.array([[1,0]]) # 観測モデルの係数行列 T = 1000 #最大時間 x0 = 0 #初期値 Tr = 0 #尤度算出のためのトリガー(Tr=1で尤度算出用) np.random.seed(seed=32) #ランダムシード固定 w = np.random.normal(0, 0.1, T) #システムノイズ(標準偏差0.1) v = np.random.normal(0, 0.2, T) #観測ノイズ(標準偏差0.2) x = np.zeros(T) #状態変数の初期化 y = np.full(T,np.nan) #観測値の初期化 # 状態変数と観測値の作成(t=310~360では観測値は得られなかったと仮定) x[0] = x0 + w[0] y[0] = x[0] + v[0] for t in range(1, T): x[t] = x[t-1] + w[t] if t < 310 or 360 < t: y[t] = x[t] + v[t] # 作成したデータの確認と保存 fig, axes = plt.subplots(nrows=1, figsize=(16, 6)) plt.title("Test Data") sns.lineplot(x=np.arange(T), y=y, color="gray", label="observation") sns.lineplot(x=np.arange(T), y=x, color="black", label="true value") axes.axvline(310, color="red", linestyle="--", alpha=0.5) axes.axvline(360, color="red", linestyle="--", alpha=0.5) plt.show() plt.show() fig.savefig("data.png", transparent = True, bbox_inches = 'tight', pad_inches = 0) |
必要なモジュールのインポートと初期値の設定とデータの作成になります。今回は時間1000stepのランダムウォークでデータを作成しました。以下のグラフが出力されます。真値が黒色、観測値が灰色です。ランダムのシード値は固定しました。
データの赤い点線の部分(310~360step)を見るとわかると思いますが、観測が行われなかったと仮定して欠損値としています(灰色が直線になっていますが、この間に観測値はありません)。
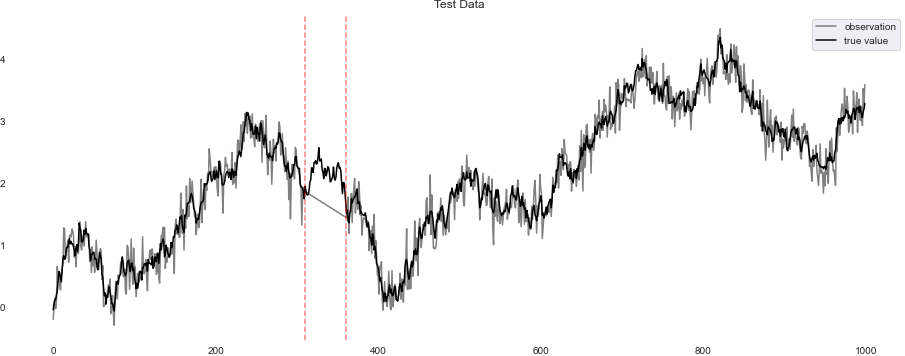
カルマンフィルタを使って観測値(灰色)から真値(黒色)を推定していきたいと思います。
2. カルマンフィルタ(1期先予測・フィルタ・平滑化)の作成
この部分はまるまる上で紹介したこちらのサイトを参考にしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
#python def kalman_prediction(a, R, W, G=G): """ Kalman prediction """ a = G @ a R = G @ R @ G.T + W return a, R def kalman_filter(m, C, y, W, V, F=F, G=G, Tr=Tr): """ Kalman Filter m: 時点t-1のフィルタリング分布の平均 C: 時点t-1のフィルタリング分布の分散共分散行列 y: 時点tの観測値 """ a = G @ m R = G @ C @ G.T + W f = F @ a Q = F @ R @ F.T + V K = (np.linalg.solve(Q.T, F @ R.T)).T m = a + K @ (y - f) C = R - K @ F @ R L = np.log(np.linalg.det(Q)) + ((y - f).T)@(np.linalg.inv(Q))@(y - f) #尤度計算のため追加 if Tr == 1: # 尤度計算のとき return m, C, L.flatten() else: # フィルタのみ実行するとき return m, C def kalman_smoothing(s, S, m, C, W, G=G): """ Kalman smoothing """ # 1時点先予測分布のパラメータ計算 a = G @ m R = G @ C @ G.T + W # 平滑化利得の計算 A = C @ G.T @ np.linalg.pinv(R) # 状態の更新 s = m + A @ (s - a) S = C + A @ (S - R) @ A.T return s, S |
上から1期先予測、フィルタ、平滑化の関数です。これだけでカルマンフィルタを実行できるなんて簡単ですね!サイトと異なるところはフィルタに尤度を計算する部分を追加したくらいです。
3. パラメータ推定(最尤推定法)
状態空間モデルの中のシステムノイズと観測ノイズははじめの状態だと未知です。ちょうどいい値を探したいのですが、このとき使うのが最尤推定法です。詳しくはこちらのサイトが良いと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# python def calcLogLike(sigma, times): # 尤度算出用 LLF = 0. # 尤度 m0 = np.array([0.0, 0.0]) # 状態変数の初期値 C0 = np.array([[1e7,0],[0,1e7]]) # 状態変数の共分散行列の初期値 m = np.zeros((T, 2)) # 状態変数 C = np.zeros((T, 2, 2)) # 状態変数の共分散行列 sigma_exp = np.exp(sigma) # システムノイズと観測ノイズの分散の値 WL = np.array([[sigma_exp[0],0],[0,0]]) # システムノイズ VL = np.array([[sigma_exp[1]]]) # 観測ノイズ for t in range(times): if t == 0: #初期 m[t], C[t], L = kalman_filter(m0, C0, y[t], W=WL , V=VL, Tr=1) LLF += -0.5*(1.*np.log(2.*np.pi) + L[0]) #尤度算出 else: if np.isnan(y[t]): # 観測値がない場合は予測を実行 m[t], C[t] = kalman_prediction(m[t-1], C[t-1], W=WL) else: m[t], C[t], L = kalman_filter(m[t-1], C[t-1], y[t], W=WL , V=VL, Tr=1) LLF += -0.5*(1.*np.log(2.*np.pi) + L[0]) #尤度算出 return -LLF # L-BFGS-B bounds = ((-40.,1.), (-20.,1.)) #変数の範囲 times = 500 #尤度算出に時刻いつまでを使うか result = scipy.optimize.minimize(calcLogLike, x0=[-10.0, -10.0], method="L-BFGS-B", bounds = bounds, args=(times,)) W1_predict = np.exp(result.x[0]) # システムノイズの分散 V1_predict = np.exp(result.x[1]) # 観測ノイズの分散 result_fun = calcLogLike(sigma=[result.x[0],result.x[1]],times = times) print('W1_predict = {0:.6g}, V1_predict = {1:.6g}, likelihood = {2:.6g}'.format(W1_predict, V1_predict, -result_fun)) # 差分進化 # bounds = ((-40.,1.), (-20.,1.)) #変数の範囲 # time = 500 #尤度算出に時刻いつまでを使うか # result = scipy.optimize.differential_evolution(calcLogLike, bounds = bounds, args=(times,)) # W1_predict = np.exp(result.x[0]) # システムノイズの分散 # V1_predict = np.exp(result.x[1]) # 観測ノイズの分散 # result_fun = calcLogLike(sigma=[result.x[0],result.x[1]],times = times) # print('W1_predict = {0:.6g}, V1_predict = {1:.6g}, likelihood = {2:.6g}'.format(W1_predict, V1_predict, -result_fun)) |
関数calcLogLikeで尤度を算出します。そしてscipyモジュールの中にある最適化アルゴリズムを使ってこの尤度を最大化(最適化アルゴリズムは最小化かので関数の戻り値はマイナスにしています)するパラメータを推定します。ポイントは欠損値がある場合には1期先予測を実行しているところです。これでおそらく欠損値を考慮した尤度が算出できると思います。
算出する期間はtimesで決めています。ながければより精度は上がると思いますが、計算に時間がかかります。このくらいだと数秒から数分だと思います。
尤度計算の方法ですが、調べてると準ニュートン法の中のL-BFGS-B法ってのが多いみたいなので、上記ではそれを使っています。ただパラメータが増えてくると局所的な解に落ちることがあったので、差分進化のコードも最後に追記しています。差分進化の方法は準ニュートン法に比べて時間はかかりますが、大域的な解にたどり着けると思います。
上記の方法で1次トレンドで算出した場合、システムノイズの分散は0.0114133、観測ノイズの分散は0.0408188、尤度は-46.9124となりました。はじめデータを作った際のシステムノイズの分散は0.01、観測ノイズの分散は0.04だったので、かなり近い値になっていると思います。
4. カルマフィルタの実行
3でパラメータが求まりましたので、カルマンフィルタを実行します。と言っても最尤推定のときにもうやってるので、同じコードになっちゃいます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# python # 初期状態のフィルタリング分布のパラメータ m0 = np.array([0.0, 0.0]) # 状態変数の初期値 C0 = np.array([[1e7,0],[0,1e7]]) # 状態変数の共分散行列の初期値 WL = np.array([[W1_predict,0],[0,0]]) # システムノイズ VL = np.array([[V1_predict]]) # 観測ノイズ m = np.zeros((T, 2)) # 状態変数 C = np.zeros((T, 2, 2)) # 状態変数の共分散行列 s = np.zeros((T, 2)) # 状態変数(カルマン平滑化用) S = np.zeros((T, 2, 2)) # 状態変数の共分散行列(カルマン平滑化用) # カルマンフィルター+カルマン予測 内容尤度算出と同じ for t in range(T): if t == 0: m[t], C[t] = kalman_filter(m0, C0, y[t], W=WL , V=VL) else: if np.isnan(y[t]): m[t], C[t] = kalman_prediction(m[t-1], C[t-1], W=WL) else: m[t], C[t] = kalman_filter(m[t-1], C[t-1], y[t], W=WL , V=VL) # カルマン平滑化 for t in range(T): t = T - t - 1 if t == T - 1: s[t] = m[t] S[t] = C[t] else: s[t], S[t] = kalman_smoothing(s[t+1], S[t+1], m[t], C[t], W=WL) |
以上でカルマンフィルタとカルマン平滑化の結果がm、Cとs、Sに格納されていると思います。
5. 図化+出力
最後の結果の図化と出力をします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
upper = 5 # y軸の上限 lower = -1 # y軸の下限 x_min = 0 # x軸の下限 x_max = 1000 # x軸の上限 legend_loc = "upper left" fig, axes = plt.subplots(nrows=3, figsize=(16, 12)) sns.lineplot(x=np.arange(T), y=y, color="gray", ax=axes[0], label="observation") sns.lineplot(x=np.arange(T), y=m[:,0].flatten(), color="red", ax=axes[0], label="kalman filter + prediction") axes[0].plot(np.arange(T), (m[:,0] - 1.96 * C[:,0,0]**(1/2)).flatten(), alpha=0.3, color='gray', label=".95 interval") axes[0].plot(np.arange(T), (m[:,0] + 1.96 * C[:,0,0]**(1/2)).flatten(), alpha=0.3, color='gray') axes[0].axvline(310, color="black", linestyle="--", alpha=0.5) axes[0].axvline(360, color="black", linestyle="--", alpha=0.5) axes[0].set_ylim(lower, upper) axes[0].set_xlim(x_min, x_max) axes[0].legend(loc=legend_loc) axes[0].set_title("Kalman Filter + Prediction") sns.lineplot(x=np.arange(T), y=y, color="gray", ax=axes[1], label="observation") sns.lineplot(x=np.arange(T), y=s[:,0].flatten(), color="green", ax=axes[1], label="kalman smoothing") axes[1].plot(np.arange(T), (s[:,0] - 1.96 * S[:,0,0]**(1/2)).flatten(), alpha=0.3, color='gray', label=".95 interval") axes[1].plot(np.arange(T), (s[:,0] + 1.96 * S[:,0,0]**(1/2)).flatten(), alpha=0.3, color='gray') axes[1].axvline(310, color="black", linestyle="--", alpha=0.5) axes[1].axvline(360, color="black", linestyle="--", alpha=0.5) axes[1].set_ylim(lower, upper) axes[1].set_xlim(x_min, x_max) axes[1].legend(loc=legend_loc) axes[1].set_title("Kalman Smoothing") # sns.lineplot(np.arange(T+K), x, ax=axes[2], label="true state") sns.lineplot(x=np.arange(T), y=y, color="gray", ax=axes[2], label="observation") sns.lineplot(x=np.arange(T), y=m[:,0].flatten(), color="red", ax=axes[2], label="kalman filter") sns.lineplot(x=np.arange(T), y=x.flatten(), color="black", ax=axes[2], label="true value") axes[2].axvline(310, color="black", linestyle="--", alpha=0.5) axes[2].axvline(360, color="black", linestyle="--", alpha=0.5) axes[2].set_ylim(lower, upper) axes[2].set_xlim(x_min, x_max) axes[2].legend(loc=legend_loc) axes[2].set_title("Kalman filter vs kalman smoothing") plt.show() fig.savefig("result.png", transparent = True, bbox_inches = 'tight', pad_inches = 0) # 出力関係 df = pd.DataFrame(np.concatenate([x.reshape(T,1), y.reshape(T,1), m[:,0].reshape(T,1), s[:,0].reshape(T,1)], 1)) df.columns=["true value", "obsevation", "kalman filter", "kalman smoothing"] df.to_csv("output.csv") |
図化したグラフがこれ
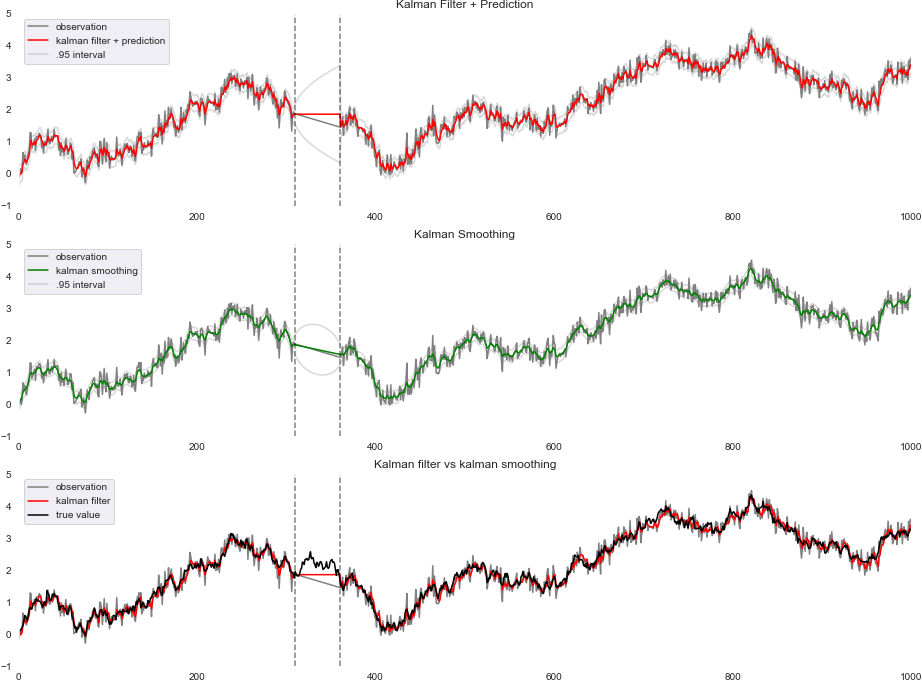
これは1次のトレンドモデルの場合です。上が観測値とフィルタ+予測、中が観測値と平滑化、下が観測値とフィルタ+予測と真値です。tが310~360の間は上を見ると分かる通り、フィルタでは同じ値が続いていますが、中に見られる通り、平滑化を行うことでなめらかに結合されています。
下を見れば分かる通りだいぶカルマンフィルタを使うことで真値に近づいたのではないでしょうか。
まとめ
今回はPythonを使って実装メインで最尤推定法によるパラメータの推定とカルマンフィルタを実施してみました。ご質問、ご指摘ございましたらコメントいただければ幸いです。
また非線形の方法についてもやっていけたらと思いますので、よろしくお願いします。
参考文献
- 時系列解析(8) −状態空間モデル−
- カルマンフィルタ・予測・平滑化で状態を逐次推定する
- 準ニュートン法による最適化とPythonによる実装
- 北側源四郎:時系列解析入門(2005)


コメント